全般
覚えることは少ない。各法則に忠実に考えることに尽きる。各法則のレベルにまで問題を細かく分ける。それができれば連立方程式のように決まった手順で解ける。
数学IIIの三角関数の微分積分と置換積分ができると理解が進む。
(このページの内容をもって問題が解けるわけではありません。問題を解くための技術は授業で教えます。)
力学
等加速度直線運動
あの3本の式に含まれる暗黙の制約に留意する。
t=0のときv=v_0 , x=0
であるからそれを満たすように座標軸の原点を設定する。2つの物体の衝突などを考える場合は2つの物体を同一座標上で扱えるように公式に一工夫する。
v^2 - v_0^2の式も積極的に使う。
運動量
運動方程式
\begin{equation*}
m\frac{dv}{dt}=F
\end{equation*}の両辺を時刻t=t_1からt=t_2まで定積分する。t=t_1のときv=v_1, t=t_2のときv=v_2とすると左辺は
\begin{equation*}
\int_{t_1}^{t_2} m \frac{dv}{dt}dt = \int_{v_1}^{v_2} mdv = mv_2 - mv_1
\end{equation*}よって
mv_2 - mv_1 = \int_{t_1}^{t_2} Fdt\int_{t_1}^{t_2} F dtは力積である。力Fが一定なら
\begin{equation*}
\int_{t_1}^{t_2} F dt = F \left( t_2 - t_1\right)
\end{equation*}であり, t_2-t_1=\Delta tとおくと
\begin{equation*}
mv_2 - mv_1 = F\Delta t
\end{equation*}力学的エネルギー保存則
ここでは重力だけを受けて鉛直方向に運動する物体を考える。鉛直上向きを正とすると物体の運動方程式は
\begin{equation*}
m\frac{dv}{dt}=-mg
\end{equation*}移項して
\begin{equation*}
m\frac{dv}{dt} + mg = 0
\end{equation*}両辺に速度v \left( =\frac{dy}{dt}\right)を掛けて両辺を不定積分する。
\begin{gather*}
mv\frac{dv}{dt} + mg\frac{dy}{dt} = 0 \\
\int mv\frac{dv}{dt}dt + \int mg\frac{dy}{dt}dt = \int 0 dt
\end{gather*}左辺は
\begin{equation*}
\int mvdv + \int mgdy = \frac{1}{2}mv^2 + mgy + C_1
\end{equation*}右辺は
\begin{equation*}
\int 0 dt = C_2
\end{equation*}C_1 , C_2は積分定数である。C_1 , C_2をまとめてCとすると
\begin{equation*}
\frac{1}{2}mv^2 + mgy = C
\end{equation*}同様に、道路上を転がる(重力の他に路面から垂直抗力を受ける)場合、ばねを含む場合、万有引力の場合も示せる。
等速円運動
円運動の半径をA, 角速度を\omegaとして物体の位置が
\begin{gather*}
x = A\cos\omega t \\
y = A\sin\omega t
\end{gather*}と表されるとする。これを時間で2回微分すると加速度であり
\begin{gather*}
a_x = -A\omega^2 \cos\omega t \\
a_y = -A\omega^2 \sin\omega t
\end{gather*}ベクトルの成分表示の形にすると加速度が常に円運動の中心を向くことが分かる。
\begin{gather*}
\vec{r} = (A\cos\omega t , A\sin\omega t) \\
\vec{a} = (-A\omega^2 \cos\omega t , -A\omega^2 \sin\omega t)
\end{gather*}よって
\begin{equation*}
\vec{a} = -\omega^2 \vec{r}
\end{equation*}さらに
\begin{equation*}
\left| \vec{a} \right| = \omega^2 \left| \vec{r} \right| = A\omega^2
\end{equation*}単振動
単振動の中心をx=x_0, 角振動数を\omegaとすると物体の位置は定数A , Bを用いて
\begin{equation*}
x = x_0 + A\cos\omega t + B \sin\omega t
\end{equation*}と表される。A , Bは問題によって決まる定数である。
\begin{equation*}
x - x_0 = A\cos\omega t + B \sin\omega t
\end{equation*}として両辺を時間で2回微分すると
\begin{equation*}
a_x = -A\omega^2 \cos\omega t - B\omega^2 \sin\omega t = -\omega^2 (x - x_0)
\end{equation*}運動方程式を作ってこの形と比較することにより角振動数、周期、振動の中心が分かる。
慣性力
乗り物の加速度を引く。
波動
縦波
変位のグラフにしたがって媒質粒子を動かして描き、粗密を再現する。
時刻がわずかに異なる2枚の変位のグラフを重ねると媒質粒子の速度が分かる。
変位と粗密、変位と速度の関係が分かるので粗密と速度の関係も分かる。
波の式
角振動数\omega=\frac{2\pi}{T}に対応して波数k=\frac{2\pi}{\lambda}がある。これを用いるとx軸の正の向きに進む波は
\begin{equation*}
y = A \sin\left( \omega t - kx\right)
\end{equation*}と表される。x軸の正の向きに進むのにsinの括弧の中が−なのが納得いかないのではないだろうか。これは2つの見方で説明できる。
まず、位置x=x_1における変位のグラフの平行移動で考える。x=x_1における変位は
\begin{equation*}
y = A \sin\left( \omega t - kx_1\right) = A \sin\left(\omega\left( t - \frac{k}{\omega}x_1\right)\right)
\end{equation*}ここで
\begin{equation*}
\frac{k}{\omega}=\frac{2\pi \times T}{\lambda \times 2\pi}=\frac{T}{\lambda}=\frac{1}{v}
\end{equation*}であるから
y = A \sin\left(\omega\left( t - \frac{x_1}{v} \right)\right)x_1>0のときはx=0における変位A\sin\omega tが\frac{x_1}{v}だけ遅れてx=x_1で観測され, x_1<0のときはx=0における変位が\frac{|x_1|}{v}だけ早くx=x_1で観測される。
よってx軸の正の向きに進む波を表している。
もう1つは位相による見方である。位相はsin, cosに与えられる角度のことで、波の新しさを表す。位相が大きいほど波は新しい。よって時間に関しては必ず+\omega tである。
位置に関してはある時刻における波の写真を考えるとよい。波がx軸の正の向きに進むならxが大きいほど波は古いので-kxになる。
屈折率
光に対して定義される絶対屈折率から始めると分かりやすい。屈折率nの媒質中を進む光の速さは真空中の\frac{1}{n}倍になる。
媒質1に対する媒質2の屈折率は割合の文章題に対応して\frac{n_2}{n_1}である。(媒質1が分母に来る。)
絶対屈折率がない波に対しても仮想的に絶対屈折率を考えることにより屈折率を含む屈折の法則の式を作れる。
熱
熱力学第一法則
仕事や熱の向きのとり方によって符号が変わるので貯金箱で考えるとよい。
電気
位置エネルギーと力の関係
位置x=x^\primeにおける位置エネルギー\phiは基準点x=cからx=x^\primeまで物体をゆっくり動かすのに必要なエネルギーで
\begin{equation*}
\phi = \int_c^{x^\prime} F_{外} dx
\end{equation*}F_{外}は手などが物体に加える力である。一方、物体が受ける重力などFは
\begin{equation*}
F = -F_{外}
\end{equation*}なので数学の
\frac{d}{dx} \int_a^x f(t) dt = f(x)より
F = -\frac{d\phi}{dx^\prime}と求められる。
重力の場合、鉛直上向きを正としてy軸をとり、原点を基準とすると位置y=y^\primeにおける位置エネルギー\phiは
\begin{equation*}
\phi = \int_0^{y^\prime} mgdy = mgy^\prime
\end{equation*}y^\primeをyに改めて
\begin{equation*}
\phi = mgy
\end{equation*}位置エネルギーから重力Fを求めるには
\begin{equation*}
F = - \frac{d\phi}{dy} = -mg
\end{equation*}静電気力の場合も同様に、点電荷Qから距離r^\primeの位置における電位は無限遠を基準にすると
\begin{equation*}
\phi = \lim_{c\rightarrow\infty}\frac{1}{q} \int_c^{r^\prime} \left( -k\frac{Qq}{r^2}\right) dr = \lim_{c\rightarrow\infty} kQ \left( \frac{1}{r^\prime}-\frac{1}{c}\right) = k \frac{Q}{r^\prime}
\end{equation*}(電位は1Cあたりのエネルギーであることに注意する。)r^\primeをrに改めて
\begin{equation*}
\phi = k \frac{Q}{r}
\end{equation*}電位は1Cあたりのエネルギーなのでq [C]のエネルギーにしてrで微分すると電荷qにかかる力は
\begin{equation*}
F = -\frac{d(q\phi)}{dr} = k \frac{Qq}{r^2}
\end{equation*}また, F = qEであるから
\begin{gather*}
qE = -\frac{d(q\phi)}{dr} \\
E = -\frac{d\phi}{dr}
\end{gather*}電束密度
\begin{equation*}
D = \epsilon E
\end{equation*}により定義される電束密度を用いるとコンデンサーの極板間に誘電体を挿入するときの電場などを容易に求められる。
境界条件
- 導体の表面、内部の電位
- 誘電率が変わる境界における電束密度
これより
- コンデンサーの電荷は極板の内側に分布すること
- コンデンサーの極板間に誘電率の異なる誘電体を積層させるときの静電容量は計算上、直列合成容量になること
などを導ける。
直列合成容量
工夫するとコンデンサーの初期の電荷が0でなくても有力な計算方法になる。
円形電流の中心における磁場
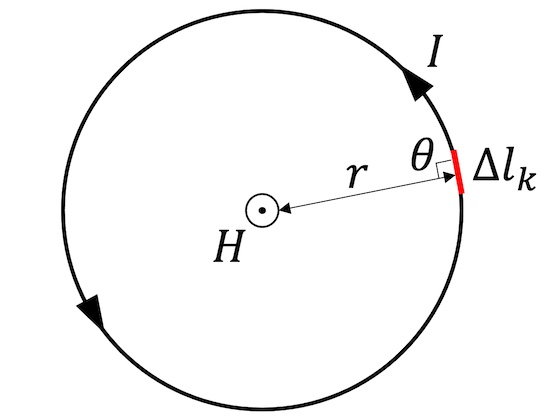
ビオ・サバールの法則による。電流Iの長さ\Delta lの部分が、それから\theta方向に距離r離れた位置に作る磁場\Delta Hは
\begin{equation*}
\Delta H = \frac{I \Delta l \sin\theta}{4\pi r^2}
\end{equation*}ただし\Delta Hの向きは右ねじの法則による。\theta=90\degreeなので
H = \sum_{k=0}^{n-1} \frac{I \Delta l_k}{4\pi r^2} = \frac{I}{4\pi r^2}\sum_{k=0}^{n-1}\Delta l_k = \frac{2\pi r I}{4\pi r^2} = \frac{I}{2r}直線電流が作る磁場、ソレノイドコイル内部の磁場
アンペアの法則から導ける。
レンツの法則
コイルは自身を貫く磁束を一定に保ちたい。
ファラデーの法則
公式の先頭のマイナスは右ねじの法則による向きの逆向きを表す。
正弦波交流の実効値
抵抗Rを負荷として交流と直流の消費電力が等しいとき、その直流電圧または直流電流を実効値という。
交流電圧
\begin{equation*}
v = V\sin\omega t
\end{equation*}を抵抗Rに加えるときの瞬時の消費電力pは
\begin{equation*}
p = \frac{V^2}{R}\sin^2\omega t = \frac{V^2}{2R}(1-\cos 2\omega t)
\end{equation*}\cos 2\omega tの平均は0なので平均の消費電力Pは
\begin{equation*}
P = \frac{V^2}{2R} = \frac{\left( \frac{V}{\sqrt{2}}\right)^2}{R}
\end{equation*}よってこの交流電圧の実効値は\frac{V}{\sqrt{2}}である。
R, L, Cの電圧と電流の関係
抵抗
\begin{equation*}
v = R i
\end{equation*}コイル、コンデンサー
\begin{gather*}
v = L \frac{di}{dt} \\
i = C \frac{dv}{dt}
\end{gather*}または
\begin{gather*}
i = \frac{1}{L} \int v dt \\
v = \frac{1}{C} \int i dt
\end{gather*}i = I \sin \omega tとすると電圧、電流の位相の違いが分かる。
さらにi = I (\cos\omega t + j \sin\omega t)(jは虚数単位)とすると凄いことが起きる。
LC共振回路
コイルの電圧、電流をそれぞれv, iとすると
\begin{gather*}
v = L \frac{di}{dt} \\
i = -C \frac{dv}{dt}
\end{gather*}iを消去すると
\begin{gather*}
v = -LC \frac{d^2 v}{dt^2} \\
\frac{d^2 v}{dt^2} = - \frac{1}{LC} v
\end{gather*}力学の単振動と同じ形で
\begin{gather*}
\omega = \frac{1}{\sqrt{LC}} \\
f = \frac{1}{2\pi\sqrt{LC}}
\end{gather*}